Create Signature

Signatures are essential for almost all features of the mmcat framework because they are needed to specify morphisms. A signature is determined by a sequence of integers, i.e. identifiers of base morphisms. But signature can be also defined as a sequence of objects.

Because of the high importance of signatures, there is a specialized tool based on the graph display tool for creating them.

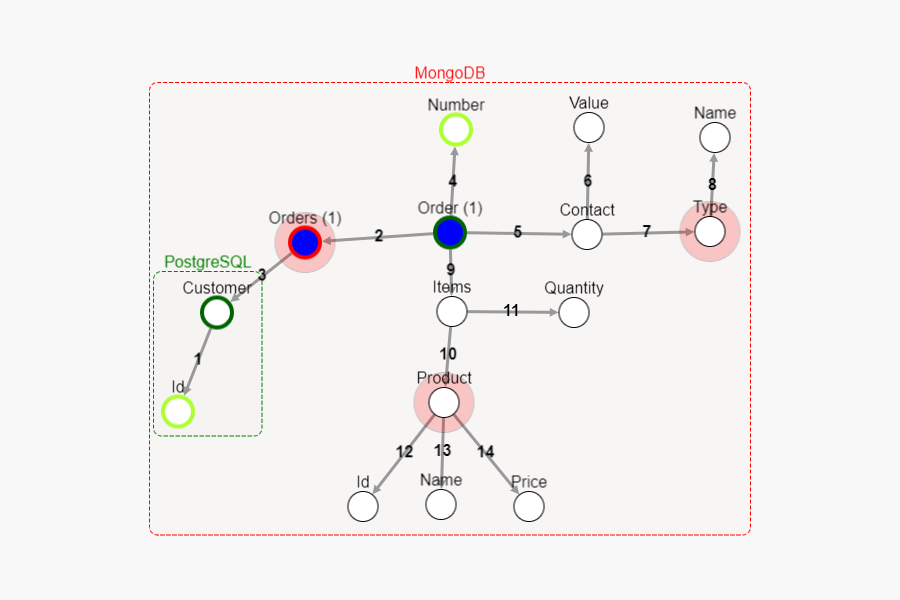
Each node in the sequence has a blue color. There is also a number in brackets in the node’s label which tells us how many times the node appears in the signature. Whenever you click on another node, it is added to the sequence (if possible).

The color of the border of the node indicates if the node can be added to the sequence:

• Black - the node is not reachable from the current sequence, so it could not be added.
• Orange - the node is reachable but the path to it is ambiguous, so it could not be added yet. This might occur when the graph contains cycles.
• Light green - there is an unambiguous path to the node, so it can be added right now.
• Dark green - same as above except the node is a direct neighbor of the last node in the sequence. There might exist other paths to the node, but the direct one will be used instead.

You can also click on the morphism arrows to add them directly to the sequence. However, this works only for the direct neighbors.

Depending on the situation the available nodes might be filtered. For example, when selecting an id for an object, a special cardinality conditions are required. If you can not create a path from one node to another, even though there are morphisms between them, check if they all satisfy these conditions.

You can add a node with ambiguous path (orange) if you specify path to it one by one using the direct neighbors (dark green) or their morphisms.

All graphs with at least two nodes are de facto ambiguous even if they do not contain explicit cycles because all morphisms have a dual in the opposite direction. So there might be any number of loops between any two nodes on the path. However, whenever you click on a green node the most direct path will be chosen.

You can create these loops, but you have to do it manually one loop at a time.

The last node in the sequence has a red border. If you click on it, it will be removed from the sequence.