Conceptual Schema

Any application needs a way to represent some sort of data. A conceptual schema is a high-level model of the data from the application’s point of view. It hides the technical details of physically storing the data from the application and allows us to concentrate on the concepts that are important for the domain we are working on. In the mmcat framework this model is represented by a schema category. A similar structure capable of holding concrete data is called instance category.

On the other hand, a logical model describes how the data should be organized to tables (for a relational model), documents (for a document model) and so on. It generally does not depend on any specific database engine. However, it might be affected by the possibilities of the target type of database systems.

The framework is based on the condition that an application should have one conceptual schema which can be mapped to multiple logical models. The models can partially or completely overlap and each of them can be suited for a different database system.

A schema category is a category, which means it is a tuple of objects, morphisms and an composition operation over the morphisms.

Each schema object corresponds to a kind or a property from the conceptual schema. It is a tuple of:

• key - an internal identifier,
• label - a user readable identifier,
• superid - a set of data attributes the object is expected to have,
• ids - a set of all identifiers of the object. Each attribute of the superid is represented by a signature of morphism that goes from the object with the superid to the object which correspond to the attribute. So the superid is just a set of signatures. The concept of signature will be explained later.

An identifier is also a set of signatures, this time their morphisms leads to the objects that unambiguously identify given object. Hence, the ids is a set of sets of signatures. It must hold that all the signatures from all the sets in the ids must be also contained in the superid.

The most simple schema object is an object with only one identifier (an empty signature) and a single element superid (also the empty signature). So its ids and superid are ${{ \epsilon }}$ and ${ \epsilon }$. This means the object represents a simple property which is identified by its value. More complex objects are identified by and contain values of other objects.

A morphism represents an oriented edge from one object to another. It is modeled as a tuple of:

• signature - an internal identifier,
• domain object - an object in which the edge starts,
• codomain object - an object in which the edge ends,
• cardinality - one of the following: 0..1, 1..1, 0..*, 1..*. In the application the signatures of base morphisms are represented by integers. The convention is that if a morphism has signature $“n”$, its dual has a signature $"-n"$. The identity morphisms are represented by the empty signature $\epsilon$.

The signatures are concatenated as follows. Consider objects $A$, $B$ and $C$ with morphisms $f: A \rightarrow B$, $g: B \rightarrow C$ and corresponding signatures $\sigma_f = \texttt{5}$, $\sigma_g = \texttt{-7}$. If we combine them to the morphism $g \circ f: A \rightarrow C$, its signature will be $$ \sigma_{g \circ f} = \sigma_g \circ \sigma_f = \texttt{-7.5} \ . $$ The domain and codomain objects are represented by their identifiers, i.e. keys.

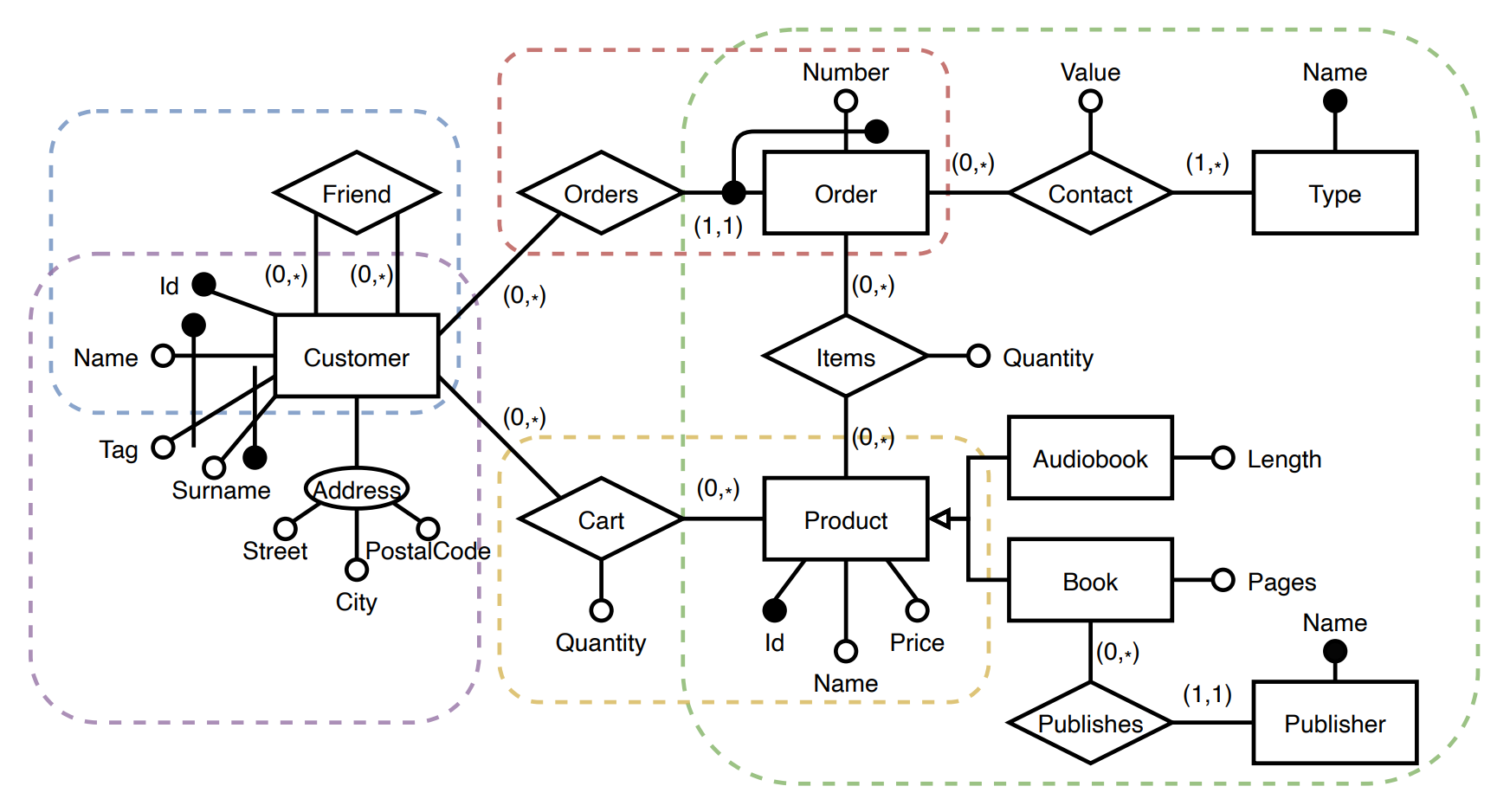
For a more complex example, here is an ER schema. The color borders define which entities are stored in which type of database:

• green - document,
• red - column,
• yellow - key-value,
• purple - relational,
• blue - graph.

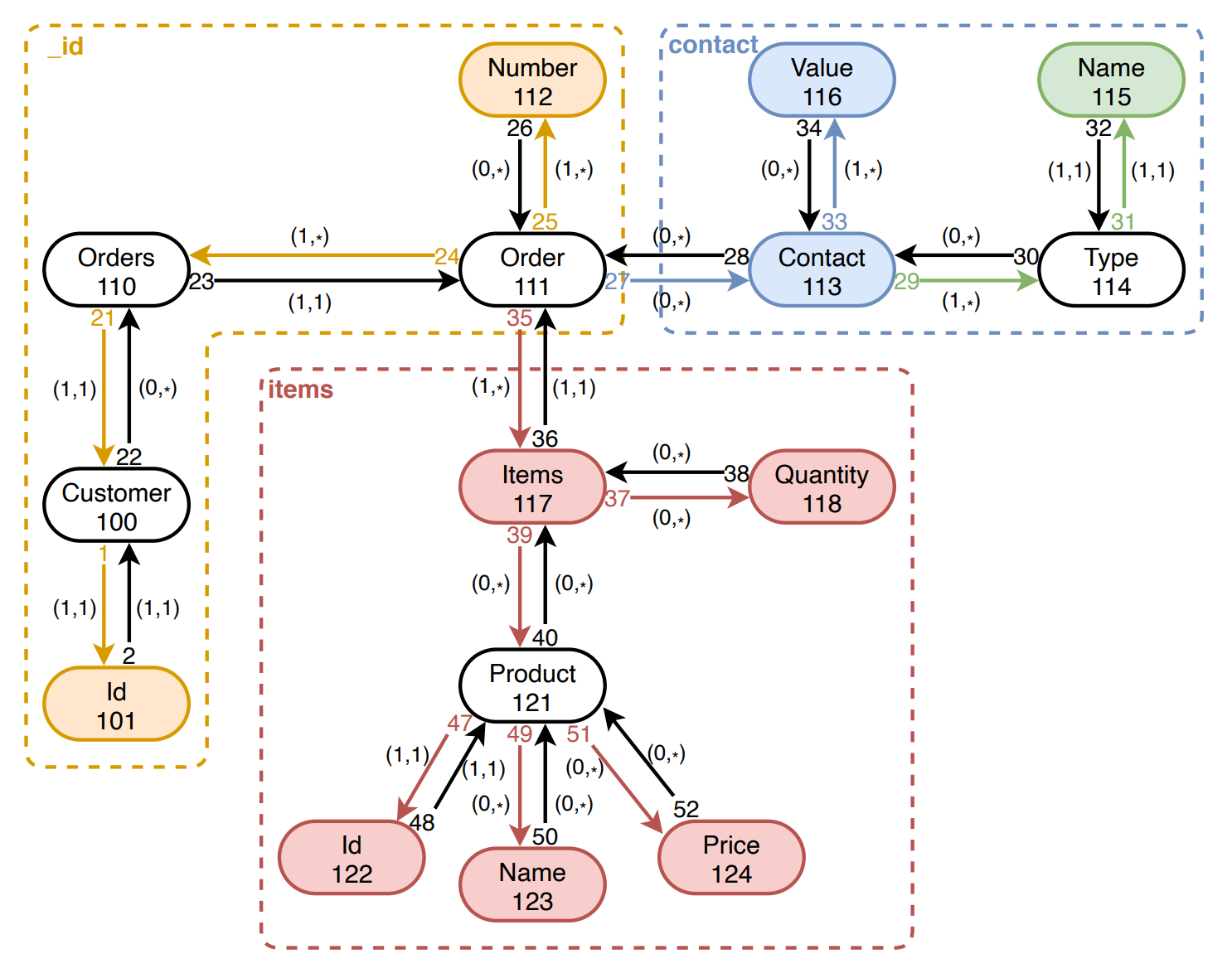
Part of the ER schema was transformed to the schema categorical representation. The resulting schema category is depicted on the next figure. The color borders there have a different meaning which will be explained in the next chapters.