Mapping

Each kind from the conceptual schema needs to be mapped to a logical model which represents data in selected database system. A mapping uses JSON-like structure called access path to both define the logical model of the kind and specify how it is mapped to the conceptual model.

Mapping also defines in which database (i.e. its type and connection credentials) is stored the data of the kind.

An access path is a tree. The root node represents the kind of the mapping. Each other node corresponds to one or no object from the schema category. The nodes that do not correspond to any object are called auxiliary.

Each edge of the access path corresponds to a morphism between the objects from the schema category to which the two nodes that are connected by the edge belong. We can represent it by putting the signature of the morphism to the child node. However, an edge between a normal node and an auxiliary one does not correspond to any morphism. Therefore, the auxiliary node gets assigned a null signature.

For example, let us consider objects $A$ and $B$ with morphism $f: A \rightarrow B$. They have corresponding nodes $n_A$ and $n_B$. Now we create an access path starting with node $n_A$ which has a child node $n$ (an auxiliary node) which has a child node $n_B$. The node $n$ will have a null signature, $n_B$ will have the signature of the morphism $f$, i.e. $\sigma_f$. Now we can find the signature of morphism from $A$ to $B$ by simply concatenating signatures from all nodes on the path from $n_A$ to $n_B$ (including $n_B$). The null signature acts effectively as an empty one, so we get $\epsilon \circ \sigma_f = \sigma_f$ which does make sense.

The last thing a node needs to be able to define mapping is a name. For a relational database, this means the name of the column. For a document one, it is the name of the property. We consider three types of names:

• Static - a string.
• Anonymous - an empty name. It has two use cases:
  • The root node of the access path.
  • A node that represents objects in an array.
• Dynamic - the name of the property corresponds to the value of another object from the schema category.

The last one might be little confusing, but it is just a way how to represent a map. For example, consider a property contact with subproperties like:

• email: example@example.com
• phone: 123456789 and similar. If the data structure is dynamic, we have no way of knowing what names these properties have. So we have to map both their values and their names in the same time.

The access path can be represented by a JSON-like structure. For example, let us consider a kind user:

{
    name: 1,        // Simple property
    address: 3.2 {  // Complex property
        ...
    },
    contact: 4 {
        6.5: 7      // Property with a dynamic name
    }
}

The first line defines a simple property with static name name and signature 1. The second line describes a complex property address with signature 2.3. This property can contain any number of other properties, for example street, city and ZIP. The contact is a complex property which contains subproperties with dynamic names. Note that those subproperties have to be contained in the contact property because they would not be recognizable from other properties (e.g. name) otherwise. Morphism with signature 6.5 defines the name of the property while 7 determines its value.

Also be aware that the cardinalities of the properties are not defined explicitly because they can be derived from the cardinalities of the morphisms instead. So if the morphism 3.2 have cardinality 0..* or 1..* the property is an array.

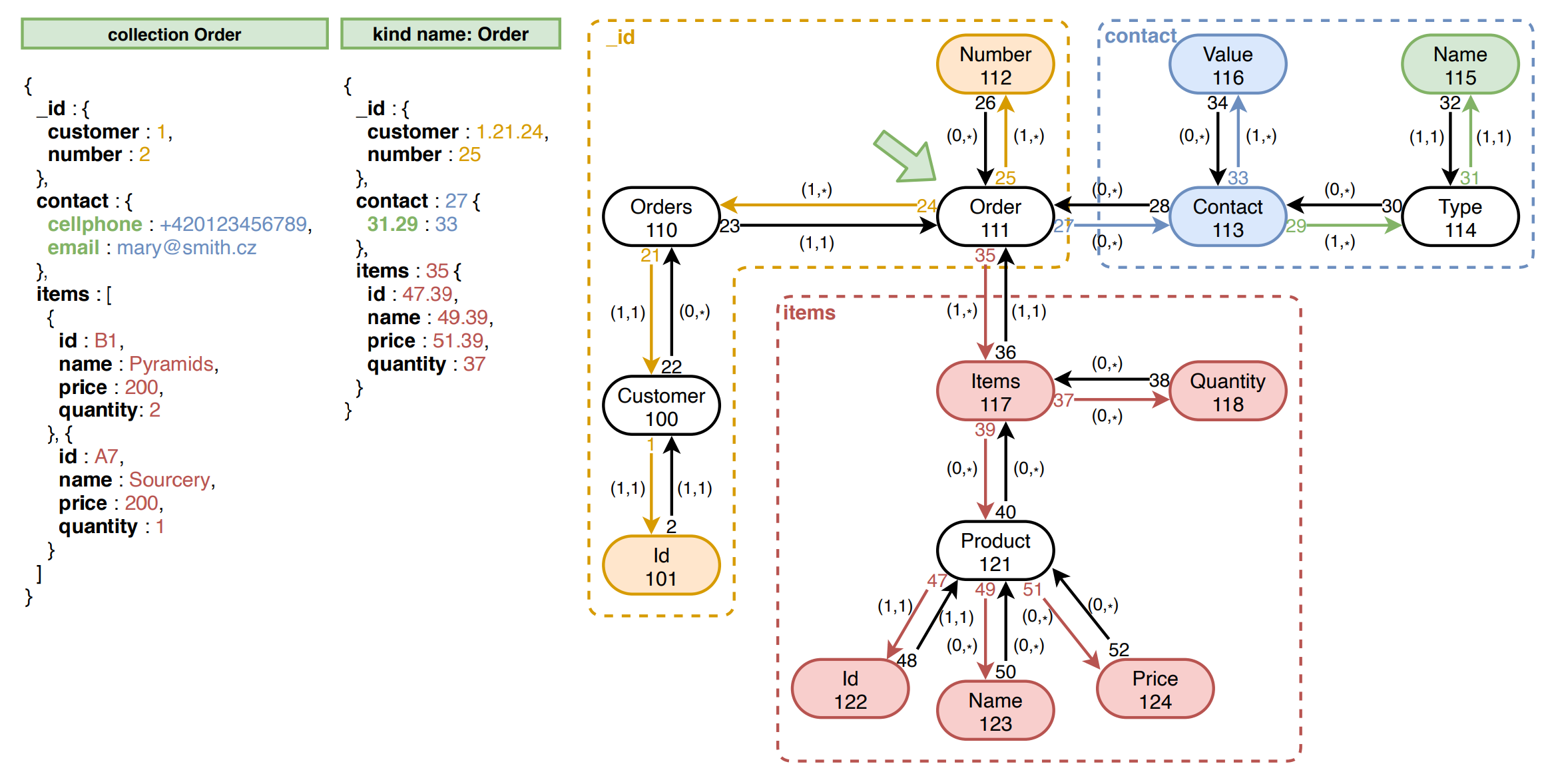
Here is an example of the schema category from one of the previous chapters. The kind Order was chosen as a root of the access path, which is shown in its JSON-like representation on in the middle of the figure. There are also some example data on the left.