Category Theory

A category consists of a set of objects, a set of morphisms and a binary composition operation over the morphisms. We can view it as a directed multigraph - the objects are the nodes and the morphisms are the oriented edges.

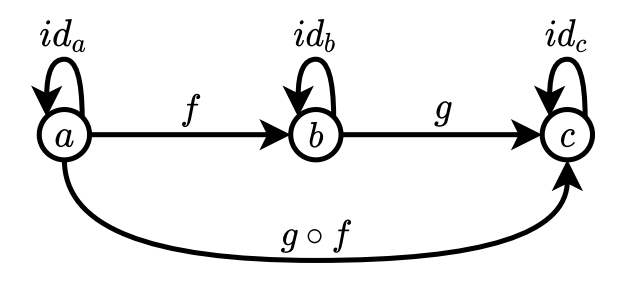
An example of a category.

The operation allows us to combine morphisms. If we have morphism $f$, i.e. an edge from object $A$ to object $B$ (which can be written as $f: A \rightarrow B$), and another morphism $g: B \rightarrow C$, we can combine them to the morphism $g \circ f: A \rightarrow C$. The whole category is closed under this operation. Also, it must hold true that chaining these operations is associative, for example $$ (h \circ g) \circ f = h \circ (g \circ f) \ . $$ Another requirement is there is an identity morphism $i_A: A \rightarrow A$ for each object $A$. The identity law must be satisfied, so $$ \begin{aligned} i_B \circ f &= f \ , \\ f \circ i_A &= f \ . \end{aligned} $$

In the mmcat framework, the direct morphisms (i.e. from one object to a different one) are called base morphisms. Those created by composition are called composite morphisms.

The current version of the framework requires that for each morphism that is not an identity morphism there is an opposite morphism (called dual). For example, if there is a morphism $f: A \rightarrow B$, there must exist a morphism $f’: B \rightarrow A$.